Animação: "Meat-A-Morphosis"
Uma introdução às funções
Legendado em português.
A Máquina de Função
para manipular números.
para manipular números.
Uma animação espirituosa de Jason Ermer, publicada em 01/2010 no Youtube, onde através de uma analogia crítica com a produção de alimentos e de fast foods, é possível compreender o conceito da função matemática f(x), e a relação entre dois elementos.
- Efetuei a tradução e a inserção das legendas, procurando preservar o significado da informação.
Link original:
Jason Ermer
Patty Hill
T. Michael Word
História:
Jason Ermer
Patty Hill
Produção:
Jason Ermer
"Um desenho animado sobre a proverbial "máquina de função" matemática. Eu fazia parte da equipe criativa de professores de matemática (incluindo Patty Hill e Michael Word) que criou este desenho animado. Ele era originalmente (e ainda é) um componente do "Honors Algebra 1" do currículo da Kealing Middle School, em Austin, Texas. Eu assumo total responsabilidade pelo erros de ortografia. (Você pode encontrá-los? :)"
Termos matemáticos curiosos da animação:
asymptote: assintótica.
- para uma curva plana, é uma linha em que a distância entre um ponto P sobre a curva e a linha aproxima-se de zero, quando a distância do ponto P à origem aumenta indefinidamente;
- para uma curva plana, é uma linha em que a distância entre um ponto P sobre a curva e a linha aproxima-se de zero, quando a distância do ponto P à origem aumenta indefinidamente;
- em ciência da computação e matemática aplicada, particularmente a análise de algoritmos, análise real, e engenharia, análise assintótica é um método de descrever o comportamento de limites.
leminscate: lemniscata.
- a Lemniscata de Bernoulli é a curva algébrica do quarto grau de equação cartesiana;
- a curva tem a forma similar ao numeral 8 e o símbolo de infinito ( ).
).
- a Lemniscata de Bernoulli é a curva algébrica do quarto grau de equação cartesiana;
- a curva tem a forma similar ao numeral 8 e o símbolo de infinito (
vinculum: vínculo.
- é o nome utilizado em inglês para o nosso famoso traço, utilizado para separar o numerador do denominador em uma fração;
- é o nome utilizado em inglês para o nosso famoso traço, utilizado para separar o numerador do denominador em uma fração;
- também é utilizado para mostrar os termos de repetição em uma fração contínua periódica;
- o vínculo foi desenvolvido no século 12 pelo matemático marroquino Abu Bakr al-Hassar.
soylent Green: trocadilho entre soy (soja) e lentil (lentilha).
soylent Green: trocadilho entre soy (soja) e lentil (lentilha).
Soylent Green
Origem: Wikipédia, a enciclopédia livre.
(br: No Mundo de 2020 / pt: À Beira do Fim) é um filme estadunidense de 1973, do gênero ficção científica, dirigido por Richard Fleischer.
(br: No Mundo de 2020 / pt: À Beira do Fim) é um filme estadunidense de 1973, do gênero ficção científica, dirigido por Richard Fleischer.
No ano de 2022, a cidade de Nova Iorque conta com 40 milhões de habitantes. Para alimentar as inúmeras pessoas pobres e desempregadas, existem tabletes verdes chamados de Soylent Green, produzidos inicialmente através da industrialização de algas. Somente os ricos tem acesso a comidas raras, como carnes, frutas e legumes. Quando um rico empresário das indústrias Soylent Corporation é assassinado em seu luxuoso apartamento, o detetive policial Robert Thorn começa a investigar. Ele de imediato suspeita do guarda-costas do empresário, que alega ter saído na hora do crime. Após interrogá-lo, Thorn vai ao apartamento dele e encontra coisas suspeitas, como uma colher com restos do caríssimo morango. Enquanto Thorn persegue o guarda-costas, seu idoso parceiro Sol começa a investigar os registros e papéis do empresário morto. E acaba descobrindo uma verdade estarrecedora.
Interpretações do filme
O segredo que o poderoso empresário conhecia colocava em risco toda a ordem social reinante, porque falava da possibilidade da destruição da vida no nosso planeta.
No estado de natureza, as mulheres bonitas foram transformadas em mobílias, a contenção das aglomerações humanas passou a desprezar os direitos individuais, os campos se tornaram em propriedade de poucos ricos e os alimentos mais banais só poderiam ser consumidos pelos que poderiam pagar por eles. O alerta continua.
Elenco principal
Elenco principal
Charlton Heston........Robert Thorn
Edward G. Robinson.....Sol Roth
Joseph Cotten..........William R. Simonson
Chuck Connors..........Tab Fielding
Leigh Taylor-Young.....Shirl
Brock Peters...........Tenente Hatcher
Origem: Wikipédia, a enciclopédia livre.
https://pt.wikipedia.org/wiki/Fun%C3%A7%C3%A3o
Função é um dos conceitos mais importantes da matemática. Existem várias definições, dependendo da forma como são escolhidos os axiomas. Uma relação entre dois conjuntos, onde há uma relação entre cada um de seus elementos. Também pode ser uma lei que para cada valor x é correspondido por um elemento y, também denotado por ƒ(x).
Algumas das funções mais conhecidas:
Injetora ou injetiva - Cada elemento da imagem está associado a apenas um elemento do domínio, isto é, quando x ≠ y no domínio tem-se f(x) ≠ f(y) no contradomínio.
Sobrejetora ou sobrejetiva - Todos os elementos do contradomínio estão associados a algum elemento do domínio.
Bijetora ou bijetiva - São ao mesmo tempo sobrejetoras e injetoras, isto é, cada elemento do domínio está associado a um único elemento do contradomínio e vice-versa.
"squinchitude":
bem... esse termo não existe...uma brincadeira no vídeo... ☺
bem... esse termo não existe...uma brincadeira no vídeo... ☺
Origem: Wikipédia, a enciclopédia livre.
https://pt.wikipedia.org/wiki/Fun%C3%A7%C3%A3o
Função é um dos conceitos mais importantes da matemática. Existem várias definições, dependendo da forma como são escolhidos os axiomas. Uma relação entre dois conjuntos, onde há uma relação entre cada um de seus elementos. Também pode ser uma lei que para cada valor x é correspondido por um elemento y, também denotado por ƒ(x).
Existem inúmeros tipos de funções matemáticas, entre as principais temos: função sobrejetora, função injetora, função bijetora, função trigonométrica, função linear, função modular, função quadrática, função exponencial, função logarítmica, função polinomial, dentre inúmeras outras. Cada função é definida por leis generalizadas e propriedades específicas.
Algumas das funções mais conhecidas:
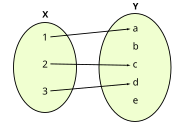 |
| Injetora ou injetiva |
 |
| Sobrejetora ou sobrejetiva |
 |
| Bijetora ou bijetiva |
Injetora ou injetiva - Cada elemento da imagem está associado a apenas um elemento do domínio, isto é, quando x ≠ y no domínio tem-se f(x) ≠ f(y) no contradomínio.
Sobrejetora ou sobrejetiva - Todos os elementos do contradomínio estão associados a algum elemento do domínio.
Bijetora ou bijetiva - São ao mesmo tempo sobrejetoras e injetoras, isto é, cada elemento do domínio está associado a um único elemento do contradomínio e vice-versa.



Nenhum comentário:
Postar um comentário